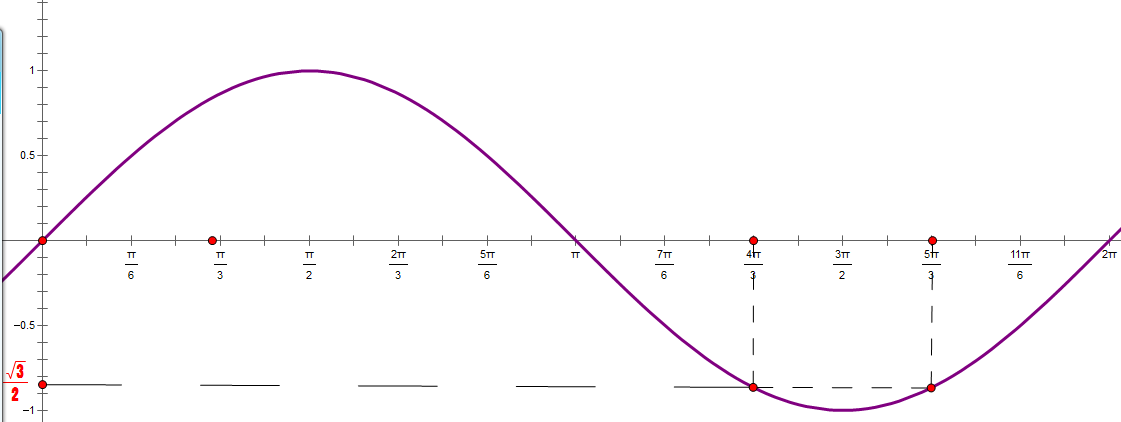
在如上坐标系中，这条正弦曲线代表的就是函数：y = a * sin(x) 中所有的点（x, y）所组成的曲线。

那么所表达的意思就是：随着x的值线性变化，y的值会在两个固定值之间来回变化，而这个固定值的大小由a来决定。

假定我们的模型左右方向是X轴，上下方向是Y轴，前后方向是Z轴，想让模型实现第一张图中的效果，就是把Z轴当做正弦函数中的y（在固定值间变化），把Y轴当做正弦函数中的x（值线性变化）。

我们将正弦函数：y = a * sin(x) 中的x和y替换：

vertice.z = WaveRange * Mathf.Sin(vertice.y + _weight);  

提供一个_weight参数，使其在0到2π间变化，这样的话就能保持我们正弦函数中的x在2π区间中变化，众所周知正弦曲线上每一个2π长度的距离内y值构成一个来回，所以这样我们的运动才会连贯。

也就是说，随着vertice.y的变化（不同顶点的y坐标自然有的不同），产生一种扭曲变化的值并赋值给vertice.z，便达到了我们想要的效果。

这里的WaveRange为正弦函数中的系数a，它的值将决定y值的变化区间，也就是我们的模型正弦运动的幅度。

总之思路就这么简单，代码都不用贴了，贴一个属性面板的说明：

FixedAxis：固定轴，正弦函数中的x分量

WaveAxis：扭动轴，正弦函数中的y分量
WaveMold：模式，Entity（正常），squash（模型压成面片）
WaveSpeed：扭动的速度
WaveRange：扭动的幅度（为0则停止扭动）
IsWaveing：开启与关闭

再贴几张效果图：