本文将由David Arppe分享一些在游戏中使用Raymarching技术的建议，以及他已用于实际游戏中的Raymarching代码。Raymarching技术实际上已经非常“古老”，在很早之前就被用于一些“古老”而经典的游戏中。例如下面两款经典的“老”游戏：

1.《Tennis for Two》（William Higinbotham，1958）



《Tennis for Two》被广泛认为是最早的视频游戏之一，它是一款使用示波器进行播放的游戏！非常酷并且很有创意！
2. 《Donkey Kong》（Nintendo Research and Development 1，1981）

《Donkey Kong》是一款诞生于视频游戏黄金年代的街机游戏。游戏主角是Jumperman（也就是现在的马里奥）。它被认为是首批带有故事情节的视频游戏之一，玩家在屏幕上可以像“看电影”一样，惊恐地看着公主一次又一次被绑架。
这些比较古老的游戏都非常有创意，他们突破了当时计算机硬件和软件的限制。超前地使用了现在仍未过时的技术。

什么是Raymarching技术

Raymarching是一种计算机图形渲染方式，但它的潜力仍未被完全发掘。Raymarching一般用于渲染体积纹理、高度图以及解析曲面。如今，大多数游戏用OpenGL或Direct3D（DirectX）来使用显卡的硬件加速器绘制多边形，电脑可以以每秒60帧的速度渲染几百万个三角面。虽然Raymarching没有那些图形API那么出名，但它可以仅用两个三角面实现无与伦比的细节。

本文的目的就是说明这种古老的渲染技术可以回归游戏了，并且使用并行处理和计算技术进行优化！

两个三角面，无限细节

RayMarching是一种数学渲染方式。它是由距离场（点到一个图元的距离）、固定步长（通常用于体积渲染）和根定位（一个数学方法）完成的。


创建上图这样的场景需要借助三维工具（Maya, Blender, 3DsMax），纹理工具（Photoshop, Gimp, MSPaint）。而该场景使用数学方法创建，使用Raymarching技术来渲染，不再受渲染三角面数的限制。不过，Raymarching技术并不是万能的，它速度较慢，有自己的方式，我认为其应该与多边形一起使用。下面的代码会给出解释。

如何在游戏中添加Raymarching

结合Raymarching与多边形两种渲染方式并不难。不过首先要理解它们之间的区别：

• Raymarching并非百分百精确。而使用距离场可以趋近于希望渲染的表面，但几乎无法得到想要的真正距离。
  渲染多边形（透视模式下）使用了投影矩阵。这是深度，不是距离。

float GetDistanceFromDepth(float2 uv, out float3 rayDir)
{
   //使用UV坐标校正空间，用于后面的矩阵算法
    float2 p = uv * 2.0f - 1.0f; // from -1 to 1    从-1到1
   //指出将深度转化为距离的参数
   //从摄像机原点到相应UV的距离
   //最近平面的坐标
    float3 rd = mul(_invProjectionMat, float4(p, -1.0, 1.0)).xyz;
 
    //创建几个变量。_ProjectionParams y 和 z分别是平面的近端和远端。
    float a = _ProjectionParams.z / (_ProjectionParams.z - _ProjectionParams.y);
    float b = _ProjectionParams.z * _ProjectionParams.y / (_ProjectionParams.y - _ProjectionParams.z);
    float z_buffer_value =  tex2D(_CameraDepthTexture, uv).r;
 
     // Z buffer数值如下：
    // z_buffer_value =  a + b / z 
 
   //计算linearEyeDepth的倒数
    float d = b / (z_buffer_value-a);
 
   //该方法也会返回射线方向，后面会用到（很重要）
    rayDir = normalize(rd);
 
    return d;
}

获得这些数据之后，将rayDir变量正规化。这很重要，因为Raymarching原理就是投射射线。

Raymarching的工作原理

在准备工作就绪后，获得深度缓存里的距离，就可以处理相交。通过逆投影矩阵计算出正确的射线，来匹配游戏中摄像机的视角。然后定位摄像机即可。

下面的代码用于控制摄像机当前位置（Unity）

fixed4 frag(v2f i) : SV_Target
{
    float3 rayDirection;
     
    float dist = GetDistanceFromDepth(i.uv.xy, rayDirection);
 
    //摄像机位置（世界坐标）
    float3 rayOrigin = _cameraPos;
 
    //计算摄像机旋转
    rayDirection = mul(_cameraMat, float4(rayDirection, 0.0)).xyz;
 
    //...
   //未完！
}

用float类型来存储距离，输出变量为float3，以便此函数输出正确的FOV，但它丢失了摄像机的旋转。可以使用标准的Uniform变量来获取这个位置（_cameraPos）。将rayDirection与视图矩阵相乘，这里w参数设为0.0是因为仅旋转摄像机，而不希望将摄像机位置存储在此变量中。

在Unity中的效果如下图，两个黄色球体与一个长方体相交。其中一个（右边的）球体使用多边形渲染。它按照预期与立方体相交。左边的球体则按设置从游戏摄像机中计算的正确FOV，位置和旋转信息。

另外请注意，与右侧多面球体相比，用Raymarching渲染球体相交的立方体表面边缘非常平滑。

渲染其它内容

使用Raymarching渲染需要较深的数学功底，下面用球体以外的形状来实现一些特殊物体！

float sdTorus( float3 p, float2 t )
{
  float2 q = float2(length(p.xz)-t.x,p.y);
  return length(q)-t.y;
}

这是一个环面的距离公式。此距离函数返回从点到距离图元最近的点的距离，将用于渲染甜甜圈。在下图中可以看到黑色图形、红圈、蓝点及红线。左下角的蓝点是摄像机，右上角的蓝点是正在观察的点。除了知道与最近平面（底部中心粗短的黑线）的距离以外没有任何信息。因此，使用这个距离来向前移动。不断重复这个过程，直到到达最终想要的平面！最后就可以得到目标平面的距离。

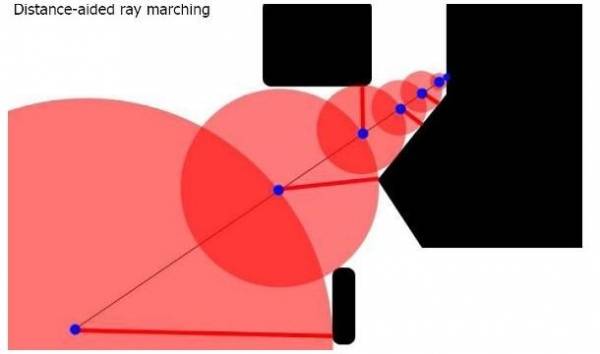
• 获取射线源（摄像机位置）
• 获取射线方向（摄像机FOV，长宽比还有旋转角度）
• 在函数中添加一个距离函数（环形）
• 将光线投射到图形上
  在该光线上获取到图形表面的距离

下面，首先要计算一个点。使用标准的point-along-a-vector方程，沿着所投射的射线移动一定的距离，然后计算到图元的距离。将刚刚计算的数值加上沿射线移动的距离，然后重复该过程。通过FOR循环进行控制。
用光线追踪这个圆环：

//将要计算的距离存储到这里
float d = 0.0f;
//将沿射线移动64次。这个数值可以改变
 
for (int i = 0; i < 64; i++)
{
   //沿射线计算前进位置的地方。初始值为rayOrigin
    float3 pos = rayOrigin + rayDirection * d;
 
   //从点到环形上最近点的距离
    float torusDistance = sdTorus(pos, float2(0.5, 0.25));
 
    d += torusDistance;
}
 
//...
//未完！

结果如下图。上面代码的作用是沿着射线进行迭代，直到获得最终距离。

现在还只渲染出纯黄色。到此已成功创建了一个环形，您也可以尝试一些其它的距离函数，并观察它们的工作工作原理。后面还会使用一些更高级的东西。

获取G-Buffer信息

还需要更多信息来使用光照模型。现在，只有一条射线的距离。要在图形上进行更多操作，需要知道：
1.3D坐标
2.表面法线
这些属性都非常容易获得！

// This is pretty self explanatory. We have the distance. We just need to move that
//有了距离后，只需沿着射线移动，就可以获取世界空间坐标
float3 pos = rayOrigin + rayDirection * d;
 
//抵消坐标的X轴，Y轴和Z轴，并将其归一化以估算表面法线
//将eps声明为float3，便于后续使用
float3 eps = float3( 0.0005, 0.0, 0.0 );
 
//可以将它封装在一个函数中。为所有的距离函数都创建一个距离字段，通常称之为“map”
#define TORUS(p) sdTorus(p, float2(0.5, 0.25)).x
float3 nor = float3(
    TORUS(pos+eps.xyy) - TORUS(pos-eps.xyy) ,
    TORUS(pos+eps.yxy) - TORUS(pos-eps.yxy) ,
    TORUS(pos+eps.yyx) - TORUS(pos-eps.yyx) );
#undef TORUS
 
nor = normalize(nor);
 
//它可以正常工作，得益于之前将结果归一化了。如果平面向上，+Y和-Y的差值将会大于+X/-X和+Y/-Y的差值。所有数据相加，将会对估算造成很大影响。从数学的角度看，是否raymarching都是估算的呢？
//...
// 未完！

结果如下图，一个有法线和世界坐标的圆环。下面来添加光照。

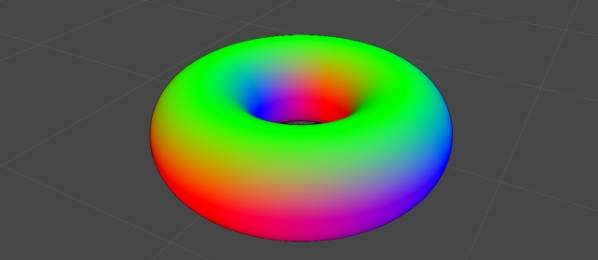
使用了标准的Phong光照模型（请参考维基百科）为圆环添加光照

// Let's create some variables to work with
//声明几个需要的变量
float3 l = normalize(sundir);   
float3 e = normalize(rayOrigin); //raymarching中，eyePos就是rayOrigin
float3 r = normalize(-reflect(l,nor));
  
//环境条件
float3 ambient = 0.3;    
 
//漫反射
float3 diffuse = max(dot(nor,l), 0.0);
diffuse = clamp(diffuse, 0.0, 1.0);     
    
//这里有一些不容易用代码编写的数值
float3 specular = 0.04 * pow(max(dot(r,e),0.0),0.2);
specular = clamp(specular, 0.0, 1.0); 
 
//现在，可以完成环形了
float4 torusCol = float4(ambient + diffuse + specular, 1.0);
 
//...
//未完

投影映射

下面在甜甜圈上撒些东西！可以在此获取所用的纹理。目标是尽可能地让它看起来更像甜甜圈。代码如下：

fixed4 frag(v2f i) : SV_Target
{
    // .. 
    //上面所有代码
    // .. 
 
   //从两个面放面团纹理。使用Z和X法线来确保不会出现不想要的颜色
    doughnutColor = tex2D(_Dough, pos.xy - float2(0.5, 0.5)).rgb * abs(nor.z);
    doughnutColor += tex2D(_Dough, pos.zy - float2(0.5, 0.5)).rgb * abs(nor.x);
 
    //从sprinkles纹理上取样，使用上下面
   //这应该是几个明显的不同情况。使用if声明
   //使用一些噪声来获得“洒”糖果的效果。
    float noiseOffset = tex2D(_Noise, pos.xz * 0.2).x * 0.5f;
    if (nor.y + noiseOffset > 0.7)
    {
        doughnutColor = tex2D(_Sprinkles, pos.xz).rgb;
    } else {
        doughnutColor += float3(1.0, 0.75, 0.5); // a color should work here //这是一种颜色
    }
 
    torusCol.rgb *= doughnutColor;
 
   //在此选用深度测试模式
 
    return (dist < d ? tex2D(_MainTex, uv) : torusCol);
}

总结
本文我们教大家Raymarching是一种计算机图形渲染方式实现了一个“甜甜圈”，是不是很有意思？当“古老”的技术与现实碰撞，有的时候能产生很不一样的效果。