Unity transform.rotation和四元数的基本理解应用

12月

13519 2

在一个同学的多次提问之下终于知道他不理解的点在哪了：
那这个四元数，具体对应到transform.rotation上，其实是。旋转轴和旋转角度的意思嘛？

属性面板设置上的rotation
是这样的，Rotation在属性面板上，那是为了方便我们直接设置角度，那三个数值是三个轴向的euler角度数。
咱们设置角度后，他会转换为四元数设置给物体的transform.rotation属性。

脚本中transform.ratation属性
而代码中的transform.ratation属性，这是一个四元数 (x, y, z, w)。
四元数是一个复数，由三个虚数，加一个实数构成。
但是不要理解为这是x,y,z坐标，w也不是旋转角度

比如物体绕Z轴旋转60度，打印出来transform.ratation就是(0.000, 0.000, 0.500, 0.866)
前面三个是与旋转轴相关的虚数，
第四个是与角度相关的实数（这只是unity中log输出，四元数的表达式第一个是实数，后面三个是虚数）
重点来了，这四个数分别是这样计算出来的：
q表示一个四元数，aix表示旋转轴向量，举个例是z轴 aix = [0 0 1]

q.w=cos(60°/2) = 0.866
q.x=Aix.x*sin(60°/2) = 0*0.5=0
q.y=Aix.y*sin(60°/2) = 0*0.5=0
q.z=Aix.z*sin(60°/2) = 1*0.5=0.5

Unity中最常用的四元数运算
(1) 四元数乘以四元数：quaternion * quaternion , 例如 q = t * p;
这是将一个点先进行t 操作旋转,然后进行p操作旋转。
(2) 四元数乘以向量：Quaternion * Vector3, 例如 p : Vector3, t : Quaternion , q : Quaternion; q = t * p;
这是将点p 进性t 操作旋转。

建议：对四元数陌生，恐惧的同学只需要借助unity中属性面板上Rotation的各轴角度，结合代码中输出 transform.rotation进行观察。
尽量先建立一个直观，并知道 x,y,z,w分别与什么相关，是怎么计算了来的，这就是一个很好的起步了！

Unity中Quaternion类最有用和最能帮助你不断增加对四元数的理解的几个方法
通过Euler方法，可以明白，如果需要 围绕X轴旋转一个50的角度，那要用Euler方法算出绕X轴转50的四元数出来：
用一个向量x,y,z的值来表示要绕这个轴旋转多少度。所以这个Vector3并不是一个坐标，而是一种哪个轴多少度的表达。

Quaternion.Euler(new Vector3(50,0,0))

通过AngleAxis方法，可以获得物体饶X轴顺时针旋转多少度后的rotation四元数：

Quaternion.AngleAxis(50,box.transform.right);

接下来我们通过一个脚本示例进行练习
代码不多但是充满思考，你一定认真看或有体会了再回来看看观察，或根据自己的理解进行修改或写代码进行尝试。

练习分三次对x,y,z轴进行旋转：box.transform.localRotation *= Euler(new Vector3(50,0,0)); 这其实就是transform带的Rotate方法中的实现，不过这只本地坐标旋转
Quaternion.eulerAngles 来一下完成三次旋转
练习用三个四元数相乘，得到完成旋转后物体的rotation四元数
练习中带有自定义的Euler，eulerAngles 方法，可以多一些理解Unity的Quaternion自带的方法里面干了什么。
不然不在预期的数字结果，会干扰你对四元数的理解。

using System;
using UnityEngine;

public class RT : MonoBehaviour
{
    public GameObject box;

    // Start is called before the first frame update
    void Start()
    {
        // 通常的x,y,z轴分三次旋转
        // 为什么叫通常的呢，因为不同软件同样是三次旋转不一定相同，
        // 比如顺序，相对轴在几次旋转中是不变还是随着物体转了轴也变，本地坐标还是世界坐标旋转，结果都是不同的
        // 比如下面的示例，分三次转和直接设置rotation = eulerAngles(new Vector3(50, 20, 60))结果是不同的
        Quaternion qx = Quaternion.AngleAxis(50,box.transform.right);
        box.transform.localRotation *= Euler(new Vector3(50,0,0));
        Quaternion qy = Quaternion.AngleAxis(20,box.transform.up);
        box.transform.localRotation *= Euler(new Vector3(0,20,0));
        Quaternion qz = Quaternion.AngleAxis(60,box.transform.forward);
        box.transform.localRotation *= Euler(new Vector3(0,0,60));

        // qxyz3与物体三次旋转后的transform.rotation相等
        // 划重点，三次旋转，可以用三个四元数相乘，
             // 但获得这三个四元数轻松，比如上面三次就每次都要获取当前物体的旋转轴，而不是用旋转开始前那个固定的旋转轴
        // 划重点，当前的四元数乘以另一个四元数，就会按这个四元数可换算出的各轴角度旋转
        // 注意以上分三次旋转，不同于直接设置rotation = eulerAngles(new Vector3(50, 20, 60))
        Quaternion qxyz3 = qz*qy*qx; // unity是z,y,z的循序相乘
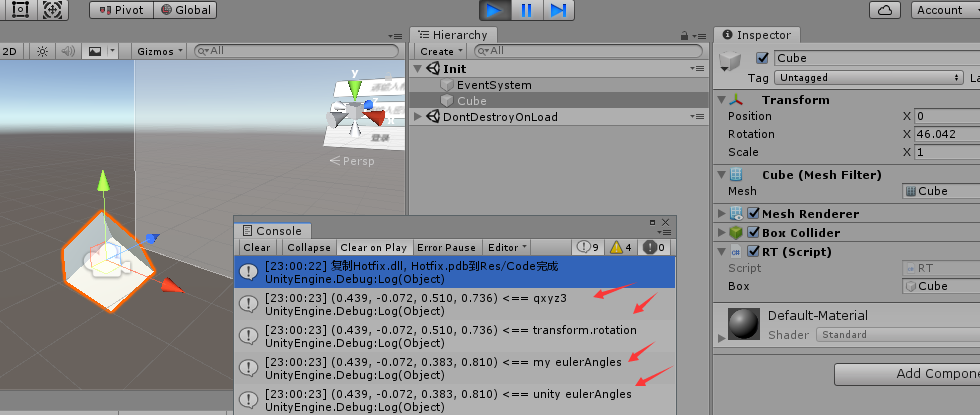
        Debug.Log($"{qxyz3.ToString("f3")} <== qxyz3");
        Debug.Log($"{box.transform.rotation.ToString("f3")} <== transform.rotation");

        // 自定义eulerAngles
        Quaternion qeuler = eulerAngles(new Vector3(50, 20, 60));
        Debug.Log($"{qeuler.ToString("f3")} <== my eulerAngles");

        // 引擎的eulerAngles
        Quaternion qeuler2 = new Quaternion();
        qeuler2.eulerAngles = new Vector3(50, 20, 60);
        Debug.Log($"{qeuler2.ToString("f3")} <== unity eulerAngles");
    }

    public Quaternion eulerAngles(Vector3 eulers )
    {
        return Euler(eulers);
    }

    public Quaternion Euler(Vector3 eulers){
        return FromEulerRad(eulers* Mathf.Deg2Rad);
    }

    // 将欧拉角转为弧度后计算完成旋转后的四元数
    public Quaternion FromEulerRad(Vector3 euler,string order = "ZYX") {
        var _x = euler.x * 0.5; // theta θ
        var _y = euler.y * 0.5; // psi ψ
        var _z = euler.z * 0.5; // phi φ

        float cX = (float)Math.Cos(_x);
        float cY = (float)Math.Cos(_y);
        float cZ = (float)Math.Cos(_z);

        float sX = (float)Math.Sin(_x);
        float sY = (float)Math.Sin(_y);
        float sZ = (float)Math.Sin(_z);

        return new Quaternion(
            sX * cY * cZ + cX * sY * sZ,
            cX * sY * cZ - sX * cY * sZ,
            cX * cY * sZ - sX * sY * cZ,
            cX * cY * cZ + sX * sY * sZ);

        // if (order == "ZXY") {
        //     return new Quaternion(
        //         cX * cY * cZ - sX * sY * sZ,
        //         sX * cY * cZ - cX * sY * sZ,
        //         cX * sY * cZ + sX * cY * sZ,
        //         cX * cY * sZ + sX * sY * cZ
        //         );
        // }

        // if (order == "XYZ") {
        //     return new Quaternion(
        //         cX * cY * cZ - sX * sY * sZ,
        //         sX * cY * cZ + cX * sY * sZ,
        //         cX * sY * cZ - sX * cY * sZ,
        //         cX * cY * sZ + sX * sY * cZ);
        // }

        // if (order == "YXZ") {
        //     return new Quaternion(
        //         cX * cY * cZ + sX * sY * sZ,
        //         sX * cY * cZ + cX * sY * sZ,
        //         cX * sY * cZ - sX * cY * sZ,
        //         cX * cY * sZ - sX * sY * cZ);
        // }

        // if (order == "ZYX") {
        //     return new Quaternion(
        //         cX * cY * cZ + sX * sY * sZ,
        //         sX * cY * cZ - cX * sY * sZ,
        //         cX * sY * cZ + sX * cY * sZ,
        //         cX * cY * sZ - sX * sY * cZ);
        // }

        // if (order == "YZX") {
        //     return new Quaternion(
        //         cX * cY * cZ - sX * sY * sZ,
        //         sX * cY * cZ + cX * sY * sZ,
        //         cX * sY * cZ + sX * cY * sZ,
        //         cX * cY * sZ - sX * sY * cZ);
        // }

        // if (order == "XZY") {
        //     return new Quaternion(
        //         cX * cY * cZ + sX * sY * sZ,
        //         sX * cY * cZ - cX * sY * sZ,
        //         cX * sY * cZ - sX * cY * sZ,
        //         cX * cY * sZ + sX * sY * cZ);
        // }
        // return new Quaternion(0,0,0,0);
    }

}